Question

Write the equation of the circle with center (-4, 8) and passes through the point (-2, -1)

Answer 1

`(x+4)^2+(y-8)^2=85`

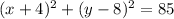
Explanation:

The standard equation for a circle is given by:

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) is the center and r is the radius.

We know that the center is (-4, 8). So, substitute -4 for h and 8 for k:

`(x-(-4))^2+(y-8)^2=r^2\\`

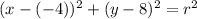
Simplify:

`(x+4)^2+(y-8)^2=r^2`

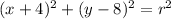
Now, we will need to find r.

We know that it passes through the point (-2, -1). So, we can substitute -2 for x and -1 for y and solve for r. So:

`(-2+4)^2+(-1-8)^2=r^2`

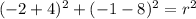
Evaluate:

`(2)^2+(-9)^2=r^2`

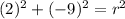
Square:

`4+81=r^2`

Add:

`r^2=85`

So, r squared is 85.

We don’t actually have to solve for r itself, since we will have to square it anyways.

So, we have:

`(x+4)^2+(y-8)^2=r^2`

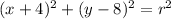
Substituting 85 for r squared, we get:

`(x+4)^2+(y-8)^2=85`

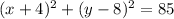
And we have our equation.