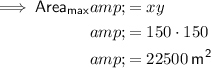Answer:
Dimensions: 150 m x 150 m
Area: 22,500m²
Explanation:
Given information:
- Rectangular field
- Total amount of fencing = 600m
- All 4 sides of the field need to be fenced
Let
 = width of the field
= width of the field
Let
 = length of the field
= length of the field
Create two equations from the given information:
Area of field:
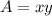
Perimeter of fence:

Rearrange the equation for the perimeter of the fence to make y the subject:
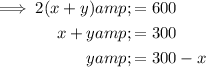
Substitute this into the equation for Area:
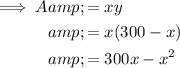
To find the value of x that will make the area a maximum, differentiate A with respect to x:
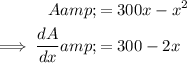
Set it to zero and solve for x:
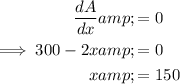
Substitute the found value of x into the original equation for the perimeter and solve for y:

Therefore, the dimensions that will give Tanya the maximum area are:
150 m x 150 m
The maximum area is: