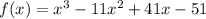Answer:
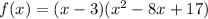
Or:
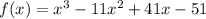
Explanation:
To find our factors, we can work backwards.
We know that 3 is a zero. This means that:
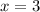
Subtract 3 from both sides:
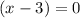
So, (x-3) is one of our factors.
We also know that (4+i) is a zero. So:
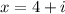
First, let’s isolate the imaginary. So, subtract 4 from both sides:
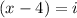
Now, let’s square both sides:
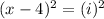
Expand the left. Evaluate the right:
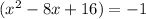
Add 1 to both sides. So, our factor is:
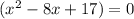
Hence, our polynomial function is:
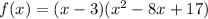
This is also the least degree since we did the most minimum we can do to solve backwards.
Further Notes:
If we want to convert this to standard form, we can distribute:
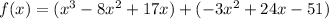
Combining like terms will yield: