Question

[solved] These Cylinders are similar. Find the volume of the smaller cylinder. Round to the nearest tenth. (the answer is 84.9 cm^3)

Answer 1

84.9 cm³

Explanation:

Height of the bigger Cylinder = 5 cm

Volume of the bigger Cylinder = 393 cm³

Height of the smaller cylinder = 3 cm

Volume of the smaller cylinder = x cm³

Since they are similar, therefore: the cube of their ratio would equal the ratio of their volume.

Thus:

`((5)/(3))^3 = (393)/(x)`

`(125)/(27) = (393)/(x)`

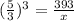
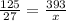
Cross multiply

`125*x = 393*27`

`125x = 10,611`

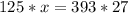
Divide both sides by 125

`(125x)/(125) = (10,611)/(125)`

`x = 84.888`

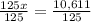
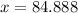
Volume of the smaller cylinder = 84.9 cm³ (to nearest tenth?