Part 6e
⇒ x² ≤ 16
Apply the absolute rule if x² < a then -√a < x < √a
⇒ -√16 ≤ x ≤ +√16
⇒ -4 ≤ x ≤ 4
Part 7
First of all, The student should have subtracted both sides by 4
What he should have done:
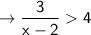
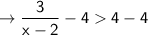
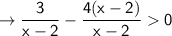
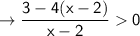
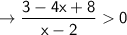
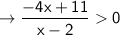
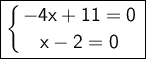
⇒ -4x + 11 = 0, x - 2 = 0
⇒ -4x = -11, x = 2
⇒ x = 11/4 , x = 2
Solution satisfying the inequality:
⇒ 2 < x < 11/4