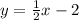Question

Write an equation in slope-intercept form that goes through (12, 4) and (20,8).

Answer 1

Equation in slope-intercept form that goes through (12, 4) and (20,8) is:
`y = (1)/(2)x-2`

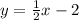
Explanation:

Given two points are:

`(x_1,y_1) = (12,4)\\(x_2,y_2) = (20,8)`

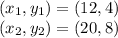
Slope intercept form of line is given as:

`y = mx+b`

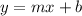
Here m is the slope of the line and b is the y-intercept.

Slope of a line is calculated by the formula:

`m = (y_2-y_1)/(x_2-x_1)`

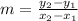
Putting the values

`m = (8-4)/(20-12)\\m = (4)/(8)\\m=(1)/(2)`

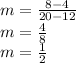
Putting the value of slope in slope-intercept form we get

`y = (1)/(2)x+b`

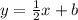
To find the value of b, any one point will be put in the equation

Putting the first point (12,4) in the equation

`4 = (1)/(2)(12) + b\\4 = 6+b\\b = 4-6\\b = -2`

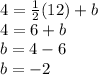
Putting the value of b

`y = (1)/(2)x-2`

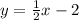
Hence,

Equation in slope-intercept form that goes through (12, 4) and (20,8) is:
`y = (1)/(2)x-2`