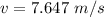Answer:
a
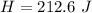
b
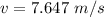
Step-by-step explanation:
From the question we are told that
The child's weight is
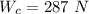
The length of the sliding surface of the playground is
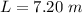
The coefficient of friction is
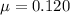
The angle is
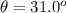
The initial speed is
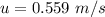
Generally the normal force acting on the child is mathematically represented as
=>
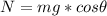
Note

Generally the frictional force between the slide and the child is
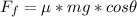
Generally the resultant force acting on the child due to her weight and the frictional force is mathematically represented as
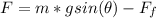
Here F is the resultant force and it is represented as
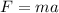
=>
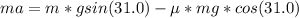
=>
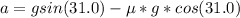
=>
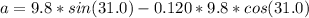
=>
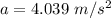
So
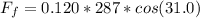
=>

Generally the heat energy generated by the frictional force which equivalent tot the workdone by the frictional force is mathematically represented as
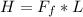
=>
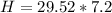
=>
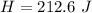
Generally from kinematic equation we have that
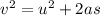
=>
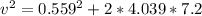
=>

=>