Question

A stone is dropped into a lake, creating a circular ripple that travels outward at a speed of 70 cm/s. Find the rate at which the area within the circle is increasing after each of the following. A. After 1 second B. After 5 seconds C. After 6 seconds

Answer 1

(A) 30772cm^2/s

(B) 153860cm^2/s

(C) 184632 cm^2/s

Explanation:

We are given

speed of the ripple = 70cm/s

this speed is increasing the radius which means speed = radius /time

radius = speed*time

r= 70t

Now we know the area of the circle

A = π
`r^2`

this area will be increasing as ripples in water will spread out

upon differentiating

dA/dt = 2πr *
`(dr)/(dt)`

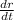
dA/dt = 2π*70t*70 ( r= 70t , dr/dt = speed = 70)

dA/dt = 9800π*t

(A) after 1 second

dA/dt = 9800π*1=9800π = 30772cm^2/s

(B) after 5 seconds

dA/dt = 9800π*5 = 153860cm^2/s

(C) after 6 seconds

dA/dt = 9800π*6 = 184632 cm^2/s