Answer:
Explanation:
From the given information:
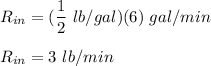
Given that the solution is pumped at a slower rate of 4gal/min
Then:
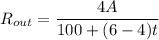

The differential equation can be expressed as:
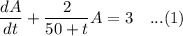
Integrating the linear differential equation; we have::
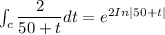

multiplying above integrating factor fields; we have:
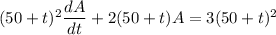
![(d)/(dt)\bigg [ (50 +t)^2 A \bigg ] = 3 (50 +t)^2](https://img.qammunity.org/2021/formulas/mathematics/college/68xc1kh6ejsyoesiikrdm1a2ixju1g2sv8.png)
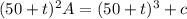
A = (50 + t) + c(50 + t)²
Using the given conditions:
A(0) = 20
⇒ 20 = 50 + c (50)⁻²
-30 = c(50) ⁻²
c = -30 × 2500
c = -75000
A = (50+t) - 75000(50 + t)⁻²
The no. of pounds of salt in the tank after 35 minutes is:
A(35) = (50 + 35) - 75000(50 + 35)⁻²
A(35) = 85 -
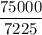
A(35) =69.6193 pounds
A(35)
 70 pounds
70 pounds
Thus; the number of pounds of salt in the tank after 35 minutes is 70 pounds.