Question

Find the approximate area under the curve by dividing the intervals into n subintervals and then adding up the areas of the inscribed rectangles. The height of each rectangle may be found by evaluating the function for each value of x. Your instructor will assign you n1and n2y = 2x underroot x^2 + 1 betwee x=0 and x=6 n1 and n2Find the exact area under the curve using integrationy = 2x underroot x^2 + 1 between x = 0 and x = 6

Explain the reason for the difference in your answers.
n1=12
n2=5

Answer 1

Answer and Step-by-step explanation: There are a number of ways of calculating an area under a curve. The more precise way is to use Definite Integral:

The function is
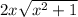`2x\sqrt{x^(2)+1}`, then the area under, with interval between 0 and 6 is:

`\int\limits^6_0 {(2x\sqrt{x^(2)+1}) } \, dx`

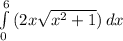
To solve this integration, use substitution method, in which:

`u=x^(2)+1`

`(du)/(dx)=2x`

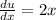
du = 2xdx

Replacing into the integral:

`\int\limits^a_b {√(u) } \, du`

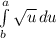
Solving:

`\int\limits^a_b {√(u) } \, du=(2)/(3) \sqrt{u^(3)}`

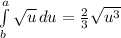
Replacing it back to x:

`\int\limits^6_0 {2x\sqrt{x^(2)+1} } \, dx =(2)/(3)\sqrt{(x^(2)+1)}`

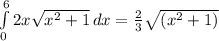
Substituing limits between 0 and 6:

`= (2)/(3)[\sqrt{(6^(2)+1)^(3)}-\sqrt{(0^(2)+1)^(3)} ]`

= 149.37

Area under the curve using Integration is 149.37 square units

Another way of calculating area under the curve is dividing the area into a number of small rectangles and then adding the area of each one. This method is called Riemann Sums and it is an approximation of the area.

The method is done by the following relation:

in which

i is the n, the number of subintervals the area is dividing into

Δx is width of each subintervals.

For the function f(x) =
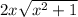`2x\sqrt{x^(2)+1}`, interval between 0 and 6:

• subinterval n1 = 12:

`\Delta x=(6-0)/(12)`

`\Delta x=` 0.5

`A=\Sigma f(x_(i)).\Delta x`

`A = f(0)*0.5+f(0.5)*0.5+f(1)*0.5+f(1.5)*0.5+f(2)*0.5+f(2.5)*0.5+f(3)*0.5+f(3.5)*0.5+f(4)*0.5+f(4.5)*0.5+f(5)*0.5+f(5.5)*0.5`

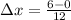
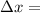`A=0+1.12*0.5+2.83*0.5+...+50.99*0.5+61.49*0.5`

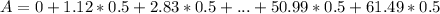
A = 131.575 square units

• subinterval n2 = 5:

`\Delta x=(6-0)/(5)`

Δx = 1.2

`A=f(0)*1.2+f(1.2)*1.2+f(2.4)*1.2+f(3.6)*1.2+f(4.8)*1.2`

`A=0*1.2+3.75*1.2+12.48*1.2+26.90*1.2+47.07*1.2`

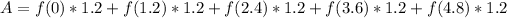
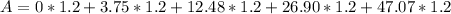
A = 108.24 square units

Comparing results, notice that with less subintervals, the area is far from the exact measure. It occurs because Riemann Sums is an approximation method. So, if there are more subintervals, more approximate is the area, therefore, more precise it will be.