Question

A random sample of 84 students at a university showed an average age of 22 years and a sample standard deviation of 3 years. Find the margin of error for the 94% confidence interval. (Assume that the population of students is large relative to the sample size. Round your solution to 4 decimal places)

Answer 1

The margin of error for the 94% confidence interval is 0.6154.

Explanation:

The (1 - α)% confidence interval for population mean is:

`CI=\bar x\pm z_(\alpha/2)\cdot(\sigma)/(√(n))`

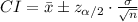
The margin of error of this interval is:

`MOE=z_(\alpha/2)\cdot(\sigma)/(√(n))`

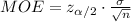
The critical value of z for 94% confidence level is, z = 1.88.

Compute the margin of error for the 94% confidence interval as follows:

`MOE=z_(\alpha/2)\cdot(\sigma)/(√(n))`

`=1.88*(3)/(√(84))\\\\=0.6154`

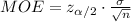
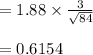
Thus, the margin of error for the 94% confidence interval is 0.6154.