Question

Using the following data, determine the percentage retained, cumulative percentage retained, and percent passing for each sieve.

Sieve size Weight retained (g) No. 4 59.5 No. 8 86.5 No. 16 138.0 No. 30 127.8 No. 50 97.0 No. 100 66.8 Pan 6.3

Answer 1

Sieve Size (in) Weight retain(g)

3 1.62

2 2.17

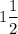`$1(1)/(2)$` 3.62

`$(3)/(4)$` 2.27

`$(3)/(8)$` 1.38

PAN 0.21

Given :

Sieve weight % wt. retain % cumulative % finer

size retained wt. retain

No. 4 59.5 10.225% 10.225% 89.775%

No. 8 86.5 14.865% 25.090% 74.91%

No. 16 138 23.7154% 48.8054% 51.2%

No. 30 127.8 21.91% 70.7154% 29.2850%

No. 50 97 16.6695% 87.3849% 12.62%

No. 100 66.8 11.4796% 98.92% 1.08%

Pan 6.3 1.08% 100% 0%

581.9 gram

Effective size = percentage finer 10% (
`$$D_(20)`)

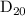0.149 mm, N 100, % finer 1.08

0.297, N 50 , % finer 12.62%

x , 10%

`$y-1.08 = (12.62 - 1.08)/(0.297 - 0.149)(x-0.149)$`

`$(10-1.08) * (0.297 - 0.149)/(12.62 - 1.08)+ 0.149=x$`

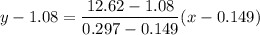
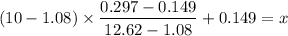
x = 0.2634 mm

Effective size,
`$D_(10) = 0.2643 \ mm$`

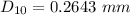
Now, N 16 (1.19 mm) , 51.2%

N 8 (2.38 mm) , 74.91%

x, 60%

`$60-51.2 = (74.91-51.2)/(2.38-1.19)(x-1.19)$`

x = 1.6317 mm

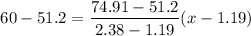
`$\therefore D_(60) = 1.6317 \ mm$`

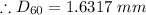
Uniformity co-efficient =
`$(D_(60))/(D_(10))$`

`$Cu= (1.6317)/(0.2643)$`

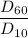
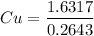
Cu = 6.17

Now, fineness modulus =
`$\frac{\Sigma \text{\ cumulative retain on all sieve }}{100}$`

`$=(\Sigma (10.225+25.09+48.8054+70.7165+87.39+98.92+100))/(100)$`

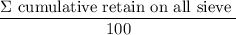
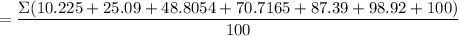
= 4.41

which lies between No. 4 and No. 5 sieve [4.76 to 4.00]

So, fineness modulus = 4.38 mm