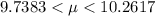Answer:
a
The upper bound of the 99% prediction level is
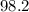
b
The 95% confidence interval is
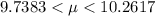
Explanation:
Considering first question
From the question we are told that
The sample size is n = 30
The sample mean is
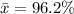
The standard deviation is
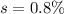
Generally the degree of freedom is mathematically represented as
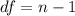
=>
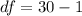
=>
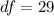
From the question we are told the confidence level is 99% , hence the level of significance is
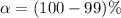
=>

Generally from the t distribution table the critical value of at a degree of freedom of is
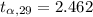
Generally the 99% prediction level is mathematically represented as
![\= x \pm [(t_(\alpha , df )) * s * (\sqrt{1 + (1)/( n) } )}]](https://img.qammunity.org/2021/formulas/mathematics/college/69g0svn3nmvepu6je121w4c0q65ora57gz.png)
Generally the upper bound of the 99% prediction level is mathematically represented as
![\= x + [(t_(\alpha , df )) * s * (\sqrt{1 + (1)/( n) } )}]](https://img.qammunity.org/2021/formulas/mathematics/college/lsnhi1n2t62mptqqio1olcpvb4tdgjvxtr.png)
=>
![96.2 + (2.462 ) * 0.8 * (\sqrt{1 + (1)/( 30) } )}]](https://img.qammunity.org/2021/formulas/mathematics/college/7h39suingjzpfin6dcgiyes33v74gbatcs.png)
=>
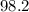
Considering second question
Generally the sample is mathematically represented as
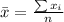
=>
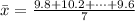
=>

Generally the standard deviation is mathematically represented as

=>
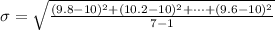
=>
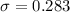
Generally the degree of freedom is mathematically represented as
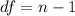
=>
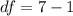
=>

From the question we are told the confidence level is 95% , hence the level of significance is
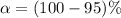
=>

Generally from the t distribution table the critical value of at a degree of freedom of is
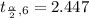
Generally the margin of error is mathematically represented as
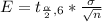
=>
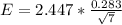
=>
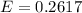
Generally 95% confidence interval is mathematically represented as
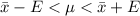
=>
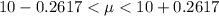
=>