Answer:
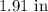
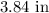
Explanation:
V = Volume of cylinder =
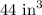
h = Height of cylinder
r = Radius of cylinder
Volume of cylinder is given by
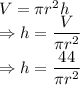
Total surface area of a cylinder is given by
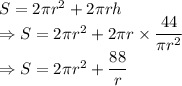
Differentiating with respect to radius
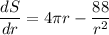
Equating with zero
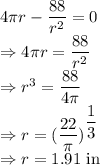
Double derivative of S
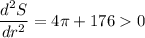
So
 is minimum at
is minimum at
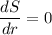
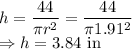
So the radius and height of the cylinder is
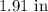 and
and
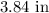 respectively such that the least amount of metal is used.
respectively such that the least amount of metal is used.