Answer:
Explained below.
Explanation:
The number of chocolate chips in an 18-ounce bag of chocolate chip cookies is approximately normally distributed with a mean of 1262 chips and standard deviation 118 chips.
(a)
Compute the probability that a randomly selected bag contains between 1000 and 1400 chocolate chips as follows:

Thus, the probability that a randomly selected bag contains between 1000 and 1400 chocolate chips is 0.8658.
(b)
Compute the probability that a randomly selected bag contains fewer than 1000 chocolate chip as follows:
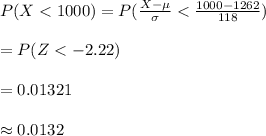
Thus, the probability that a randomly selected bag contains fewer than 1000 chocolate chip is 0.0132.
(c)
Compute the proportion of bags that contains more than 1200 chocolate chips as follows:
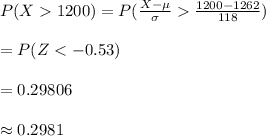
Thus, the proportion of bags that contains more than 1200 chocolate chips is 0.2981.
(d)
Compute the percentile rank of a bag that contains 1125 chocolate chips as follows:
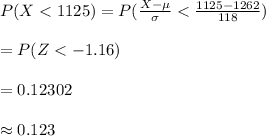
Thus, the percentile rank of a bag that contains 1125 chocolate chips is 12.3rd.