Question

According to the U.S. Census Bureau, 20.2% of American women aged 25 years or older have a Bachelor's Degree; 16.5% of American women aged 25 years or older have never married; among American women aged 25 years or older who have never married, 22.8% have a Bachelor's Degree; and among American women aged 25 years or older who have a Bachelor's Degree, 18.6% have never married.

Required:
a. Are the events "have a Bachelor's Degree" and "never married" independent? Explain.
b. Suppose an American woman aged 25 years or older is randomly selected, what is the probability she has a Bachelor's Degree and has never married? Interpret this probability.

Answer 1

(a) Not independent

(b) The probability the woman has a Bachelor's Degree and has never married is 0.046.

Explanation:

Denote the events as follows:

X = American women aged 25 years or older have a Bachelor's Degree

Y = American women aged 25 years or older have never married

The information provided is as follows:

P (X) = 0.202

P (Y) = 0.165

P (X | Y) = 0.228

P (Y | X) = 0.186

(a)

If two events, say A and B are independent then,

P (A|B) = P (A) and P (B|A) = P (B)

Since,

P (X | Y) ≠ P (X)

P (Y | X) ≠ P (Y)

The events "have a Bachelor's Degree" and "never married" are not independent.

(b)

Compute the probability the woman has a Bachelor's Degree and has never married as follows:

`P(X\cap Y)=P(X|Y)* P(X)\\\\=0.228* 0.202\\\\=0.046056\\\\\approx 0.046`

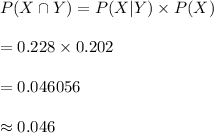
Thus, the probability the woman has a Bachelor's Degree and has never married is 0.046.