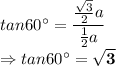Question

What is the value of tan(60°)? One-half StartRoot 3 EndRoot StartFraction StartRoot 3 EndRoot Over 2 EndFraction StartFraction 1 Over StartRoot 3 EndRoot EndFraction

Answer 1

Answer: the answer is
`√(3)`

Step-by-step explanation: I got it correct. it is show below.

Answer 2

`\sqrt3`

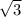
Explanation:

To find:

The value of
`tan60^\circ` = ?

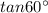Solution:

Kindly consider the equilateral
`\triangle ABC` as attached in the answer area.

Let the side of triangle =
`a` units

Let us draw the perpendicular from vertex A to side BC.

It will divide the side BC in two equal parts.

i.e. BD = DC =
`(a)/(2)`

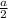
Using Pythagorean Theorem in
`\triangle ABD`:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)`

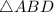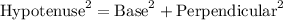
Side AD =
`(\sqrt3)/(2)a`

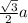
Using Trigonometric ratio:

`tan\theta = (Perpendicular)/(Base)`

`tanB = (AD)/(BD)`

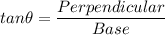
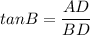
Putting the values of AD and BD:

`tan60^\circ=((\sqrt3)/(2)a)/((1)/(2)a)\\\Rightarrow tan60^\circ = \bold{\sqrt3}`