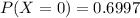Answer:
The probability is
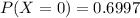
Explanation:
From the question we are told that
The mean is
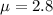
Generally the Poisson distribution constant
 is mathematically represented as
is mathematically represented as
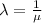
=>

=>

Generally the probability distribution for Poisson distribution is mathematically represented as
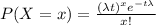
Here t = 1 day
Generally the probability that no babies are born today is mathematically represented as
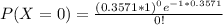
=>