Question

In October of 2019, Gallup asked a random sample of 1,506 Americans which of two approaches to punishing murder they thought was better, the death penalty or life without possibility of parole. For the first time since Gallup began asking the question in 1985, a majority of Americans now say life imprisonment is a better approach for punishing murder than is the death penalty. According to the 2019 Gallup death-penalty poll, 60% percent of Americans asked to choose whether the death penalty or life without possibility of parole "is the better penalty for murder" chose the life-sentencing option. 36% favored the death penalty.

Required:
a. Find a 95% confidence interval for the proportion adults in the US that now believe life imprisonment is a better approach for punishing murder.
b. Interpret your interval above in the context of this problem.
c. Use your interval to find the margin of error associated with this confidence interval.
d. If we increase the level of confidence to 98%, will the interval be wider or narrower?

Answer 1

a

The 95% confidence interval is
`0.5753<  p <0.62474`

b

This 95% confidence interval tell us that there 95% confidence that the true proportion of adults in the US that now believe life imprisonment is a better approach for punishing murder lies within the interval

c

The margin of error is
`E =    0.02474`

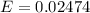
d

The confidence interval becomes wider

Explanation:

From the question we are told that

The sample size is n = 1506

The sample proportion is
`\^ p = 0.60`

From the question we are told the confidence level is 95% , hence the level of significance is

`\alpha = (100 - 95 ) \%`

=>
`\alpha = 0.05`

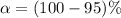
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  1.96`

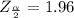
Generally the margin of error is mathematically represented as

`E =  Z_{(\alpha )/(2) } * \sqrt{(\^ p (1- \^ p))/(n) }`

=>
`E =    1.96 * \sqrt{(0.60 (1- 0.60))/(1506) }`

=>
`E =    0.02474`

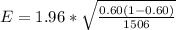
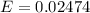
Generally 95% confidence interval is mathematically represented as

`\^ p -E <  p <  \^ p +E`

=>
`0.60 - 0.02474 <  p <0.60 + 0.02474`

=>
`0.5753<  p <0.62474`

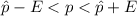
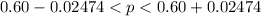
This 95% confidence interval tell us that there 95% confidence that the true proportion of adults in the US that now believe life imprisonment is a better approach for punishing murder lies within the interval

Generally the level of confidence varies directly with the critical value of
`(\alpha )/(2)` and this in turn varies directly with the margin of error which when sample proportion is constant it determines the width of the confidence interval so when the level of confidence increases the confidence interval becomes wider