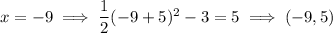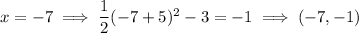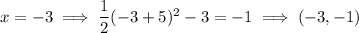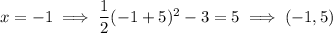Answer:
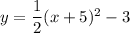
Explanation:
Translations
For
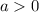
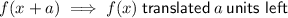

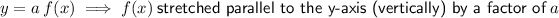
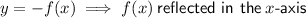
Parent function
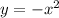
Reflected in the x-axis
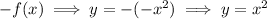
Compressed vertically by a factor of 1/2
Multiply the whole function by the given scale factor:
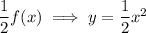
Translated 3 units down
Subtract 3 from the whole function:
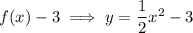
Translated 5 units left
Add 5 to the variable of the function:
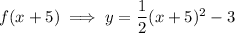
To sketch the parabola
Vertex =
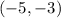
Axis of symmetry:

Plot points: