Question

Find the expected value and the variance of the number of times one must throw a die until the outcome 1 has occurred 5 times.

Answer 1

Answer: E(X) = 30; Var[X] = 180

Explanation: This is a Bernoulli Experiment, i.e., the experiment is repeated a fixed number of times, the trials are independents, the only two outcomes are "success" or "failure" and the probability of success remains the same, So, to calculate Expected Value, which is the mean, in these conditions:

`E(X)=(r)/(p)`

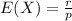
r is number of times it is repeated

p is probability it happens

Solving:

`E(X)=(5)/(1/6)`

E(X) = 30

Variance is given by:

`Var[X]=(r(1-p))/(p^(2))`

`Var[X]=(5(1-1/6))/((1/6)^(2))`

`Var[X]=5.(5)/(6).6^(2)`

Var[X] = 180

Expected Value and Variance of the number of times one must throw a die until 1 happens 5 times are 30 and 180, respectively.