Question

A young couple purchases their first new home in 2011 for​ $95,000. They sell it to move into a bigger home in 2018 for​ $105,000. First, we will develop an exponential model for the value of the home. The model will have the form

Answer 1

Given:

The value of home in 2011 is $95,000.

The value of home in 2018 is $105,000.

To find:

The exponential model for the value of the home.

Solution:

The general exponential model is

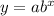`y=ab^x` ...(i)

where, a is initial value and b is growth factor.

Let 2011 is initial year and x be the number of years after 2011.

So, initial value of home is 95,000, i.e., a=95,000.

Put a=95000 in (i).

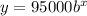`y=95000b^x` ...(ii)

The value of home in 2018 is $105,000. It means the value of y is 105000 at x=7.

`105000=95000b^7`

`(105000)/(95000)=b^7`

`(21)/(19)=b^7`

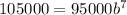
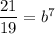
Taking 7th root on both sides, we get

`\left((21)/(19)\right)^{(1)/(7)}=b`

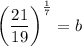
Put
`b=\left((21)/(19)\right)^{(1)/(7)}` in (ii).

`y=95000\left(\left((21)/(19)\right)^{(1)/(7)}\right)^x`

`y=95000\left((21)/(19)\right)^{(x)/(7)}`

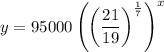
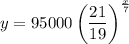
Therefore, the required exponential model for the value of home is
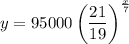`y=95000\left((21)/(19)\right)^{(x)/(7)}`, where x is the number of years after 2011.