Question

• You have given an equal sided triangle with side length a. A straight line connects the center of the bottom side to the border of the triangle with an angle of α. Derive an expression for the enclosed area A(α) with respect to the angle (see drawing).

Answer 1

9514 1404 393

Answer:

`A(\alpha)=\left\{\begin{array}{ccc}\frac{a^2√(3)sin((\alpha))}{16\sin{(\alpha+(\pi)/(3))}}&\text{if $\alpha\le(\pi)/(2)$}\\\\(a^2√(3))/(4)\left(1-\frac{sin((\alpha))}{4\sin{(\alpha-(\pi)/(3))}}\right)&\text{if $\alpha>(\pi)/(2)$}\end{array}\right.`

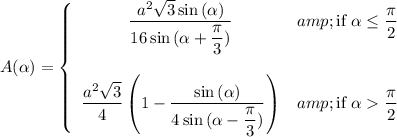
Explanation:

If we place the bottom center at the origin and make the sides of the triangle 2 units, then the right side can be described by the equation ...

y = √3(1 -x)

and the terminal side of the angle α can be described by ...

y = tan(α)·x

We want the height of the shaded area, which is the y-coordinate of the point of intersection of these two lines.

y = √3(1 -y/tan(α)) . . . . substituting for x

y = √3·tan(α)/(√3 +tan(α)) . . . . solved for y

Since we have defined the base of the shaded area to be 1, the shaded area is half this value, or ...

A(α) = (√3/2)tan(α)/(√3 +tan(α))

Further manipulation can put this in the form ...

A(α) = (√3/4)sin(α)/sin(α+π/3) . . . . for α ≤ π/2, side length 2

__

For α > π/2, we need to subtract the area A(π-α) from the area of the whole triangle. This gives an area (after some rearranging) of ...

A(α) = √3(1 -sin(α)/(4·sin(α-π/3))) . . . . for α > π/2, side length 2

__

The problem statement defines the triangle as having a side length of 'a', so the final area formula will be a factor of (a/2)² times the above expressions. That is ...

`A(\alpha)=\left\{\begin{array}{ccc}\frac{a^2√(3)sin((\alpha))}{16\sin{(\alpha+(\pi)/(3))}}&\text{if $\alpha\le(\pi)/(2)$}\\\\(a^2√(3))/(4)\left(1-\frac{sin((\alpha))}{4\sin{(\alpha-(\pi)/(3))}}\right)&\text{if $\alpha>(\pi)/(2)$}\end{array}\right.`

_____

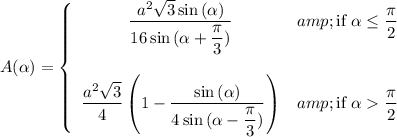
The graph (second attachment) shows the area as a function of α (in degrees) for a unit triangle. There are inflection points in the curve at 30°, 90°, and 150°