Question

Una escalera de 131313 metros está recargada contra una pared cuando su base empieza a resbalar. Cuando la base está a 121212 metros de la pared, se mueve a una razón de 5\text{ m/s}5 m/s5, start text, space, m, slash, s, end text. En ese momento, ¿a qué razón está cambiando el ángulo \thetaθtheta entre el piso y la escalera?

Answer 1

El ángulo entre el piso y la escalera está cambiando a una razón de -1 radian por segundo.

Explanation:

Sea
`x` la distancia horizontal entre la pared y la base de la escalera y
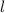`l` la longitud de la escalera, medidas en metros. Además, tenemos que
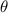`\theta` es el ángulo entre la escalera y el piso, medido en radianes.

Si la pared y el piso son ortogonales entre sí, entonces podemos utilizar la siguiente relación trigonométrica que relaciona las variables anteriores:

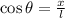`\cos \theta = (x)/(l)` (1)

Por diferenciación implícita y la definición de razón de cambio tenemos que:

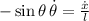`-\sin \theta \,\dot \theta = (\dot x)/(l)` (2)

Donde:

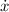`\dot x` - Razón de cambio de la distancia horizontal entre la pared y la base de la escalera, medida en metros por segundo.

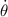`\dot \theta` - Razón de cambio del ángulo entre el piso y la escalera, medida en radianes por segundo.

Pero tenemos que el seno del ángulo está definido por:

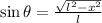`\sin \theta = \frac{\sqrt{l^(2)-x^(2)}}{l}` (3)

Si aplicamos (3) en (2), expandimos la ecuación como sigue:

`-\frac{\sqrt{l^(2)-x^(2)}}{l}\,\dot \theta = (\dot x)/(l)`

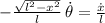
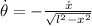`\dot \theta = - \frac{\dot x}{\sqrt{l^(2)-x^(2)}}` (4)

Si tenemos que
`\dot x = 5\,(m)/(s)`,
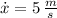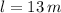`l = 13\,m` y
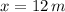`x = 12\,m`, entonces la razón de cambio del ángulo es:

`\dot \theta = -\frac{\left(5\,(m)/(s) \right)}{\sqrt{(13\,m)^(2)-(12\,m)^(2)}}`

`\dot \theta \approx -1\,(rad)/(s)`

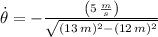
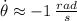
El ángulo entre el piso y la escalera está cambiando a una razón de -1 radian por segundo.