Question

An electron with a total energy of 19GeV travels through an accelerator tube with proper length 7.7km. a) What is the length of the tube in the electron's frame? E= m b) How long does it take in the frame of the electron? E= s c) How long does it take in the frame of the tube? T= s Note: the rest energy of an electron is: 0=0.51MeV.

Answer 1

a) Approximately 0.2066 m

b) 0.00002568443 s

c) Approximately 188.87 s

Step-by-step explanation:

a) The total energy of the electron = 190GeV

The rest energy of the electron = 0.51 MeV

`(19 \ GeV)/(0.51 \ MeV) = 37254.902 = \frac{1}{\sqrt{1 + (u^2)/(c^2) } }`

`\left ( 1 - (u^2)/(c^2) \right ) = (1)/(37254.902^2) } }`

`\left ( 1 - (1)/(37254.902^2) } } \right ) = (u^2)/(c^2)`

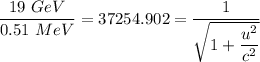
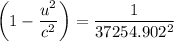
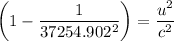
u = √(299792458² × (1 - 1/37254.902²)) = 299792457.892

β = v/c = 299792457.892/299792458 = 0.99999999964

`\beta = \sqrt{1 - \left ( (\Delta x)/(\Delta x') \right )^2}`

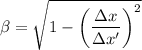
Δx = √(Δx'²×(1 - β²)) = √(7700²×(1 - 0.99999999964²)) ≈ 0.2066 m

The length of the tube in the electron's frame ≈ 0.2066 m

b) The time in the frame of the electron is given as follows;

Δt' = 7700/299792457.892 = 0.00002568443 s

c) The time in the frame of the tube is given as follows;

`\beta = \sqrt{1 - \left ( (\Delta t')/(\Delta t) \right )^2}`

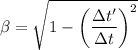
1 - β² = (Δt'/Δt)²

Δt = √(Δt'/(1 - β²)) = √(0.00002568443 /(1 - 0.99999999964²)) ≈ 188.87 s.