Question

A planet similar to the Earth has a radius 5 × 106 m and has an acceleration of gravity of 10 m/s 2 on the planet's surface. The planet rotates about its axis with a period of 25 h. Imagine that the rotational speed can be increased. If an object at the equator is to have zero apparent weight, what is the new period? Answer in units of h.

Answer 1

The new period is approximately 3.93 × 10⁻⁷ h

Step-by-step explanation:

The radius of the planet = 5 × 10⁶ m

The acceleration due to gravity on the planet, a = 10 m/s²

The period of the planet = 25 h

The centripetal force,
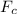`F_c`, is given by the following equation;

`F_c = (m \cdot v^2)/(r)`

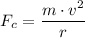
Where;

v = The linear speed

r = The radius

Therefore, for the apparent weight, W, of an object to be zero, we have;

The weight of the object = The centripetal force of the object

W = Mass, m × Acceleration due to gravity, a

∴ W =
`F_c`

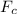
Which gives;

`m * a = (m \cdot v^2)/(r)`

`a = (v^2)/(r)`

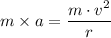
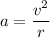
∵ r = The radius of the planet

We have;

`10 = (v^2)/(5 * 10^6)`

v² = 10 × 5 × 10⁶

v = √(10 × 5 × 10⁶) ≈ 7071.07 m/s

The new frequency = Radius of the planet/(Linear speed component of rotation)

∴ The new frequency = 5 × 10⁶/(7071.07) = 707.107 revolutions per second

The new frequency = 707.107 × 60 × 60 = 2545585.2 revolutions per second

The new period = 1/Frequency ≈ 3.93 × 10⁻⁷ hour.