Answer:
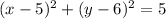
Explanation:
Equation of the Circle
A circle centered at (h,k) and radius r can be written with the equation:

We are given the center (5,k), thus:
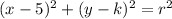
We know the point (3,7) belongs to the circle. This means the distance between the center and this point is the radius.
Given two points (x1,y1) and (x2,y2), the distance between them satisfies:
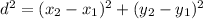
Calculating the radius, we have:
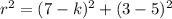
![r^2=(7-k)^2+4\qquad\qquad [1]](https://img.qammunity.org/2021/formulas/mathematics/high-school/6lk0wa8k5l2m9jz56k1fno5m3wkht0ssum.png)
Now we use the fact that the line y=2x+1 and the circle are tangent at (3,7). The radius and the line are perpendicular at that point. Two perpendicular lines with slopes m1 and m2 satisfy the condition:
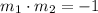
The line y=2x+1 has a slope of m1=2, thus the slope of the segment from (5,k) to (3,7) has a slope of -1/2:
The slope is calculated as:
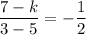
Operating:
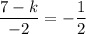
Multiplying by -2
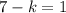
Solving:
k=6
From [1] the radius is:
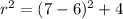
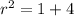

Finally, substituting into the equation of the circle:
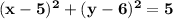
The graph can be seen in the figure below.