Answer:
The equation is y = 2x² + 7x + 5
Explanation:
In the quadratic equation y = ax² + bx + c
- The roots of it are the values of x at y = 0
- The sum of the two roots =
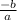
- The product of the two roots =
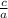
∵ The sum of the roots is
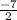
∵ The product of the roots is
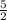
→ By using the rules above
∴
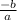 =
=
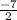
∴
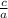 =
=
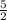
→ Compare between them
∴ a = 2
∴ -b = -7 ⇒ divide both sides by -1
∴ b = 7
∴ c = 5
∵ The form of the quadratic function is y = ax² + bx + c
→ Substitute the values of a, b, and c in it
∴ y = 2x² + 7x + 5
∴ The equation is y = 2x² + 7x + 5