Question

A certain bacteria multiply exponentially at a rate of 8% per day. If 2 bacteria exist initially, how many

will be present after 25 days?

Answer 1

After 25 days will be present about 13.70 ≅ 13 bacteria

Explanation:

The form of the exponential function is y = a
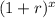`(1+r)^(x)` , where

• a is the initial value

• r is the rate in decimal

∵ A certain bacteria multiply exponentially at a rate of 8% per day

→ Assume that y is the number of bacteria, x is the number of days

∴ r = 8% =
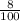`(8)/(100)` = 0.08

∵ 2 bacteria exist initially

∴ a = 2

→ Substitute them in the form of the equation above

∵ y = 2
`(1+0.08)^(x)`

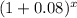
∴ y = 2
`(1.08)^(x)`

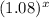
∵ x = 25

→ Substitute x in the equation by 25

∴ y = 2
`(1.08)^(25)`

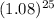
∴ y = 13.69695

∴ After 25 days will be present about 13.70 bacteria

Note: The number of bacteria must be the whole number so the answer should be 13 bacteria will be present after 25 days.