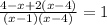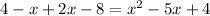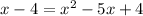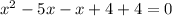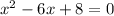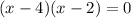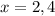Question

(4-x)/(x^2-5x+4)+(2)/(x-1)=1

show all steps please!!

Answer 1

`x = 2, 4`

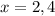
Explanation:

Given :

`(4-x)/(x^(2) -5x+4) + (2)/(x-1) =1`

=============================================================

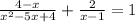
Factorize the denominator of the first term :

⇒ x² - 5x + 4

⇒ x² - x - 4x + 4

⇒ x(x - 1) - 4(x - 1)

⇒ (x - 4)(x - 1)

============================================================

Hence, the equation now is :

`(4-x)/((x-1)(x-4)) + (2)/(x-1) =1`

============================================================

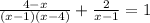
Multiply the second term by (x - 4) in the numerator and denominator :

`(4-x)/((x-1)(x-4)) + (2(x-4))/(x-1(x-4)) =1`

============================================================

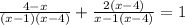
Combine the numerator of both terms and bring the denominator to the other side :

`(4-x+2(x-4))/((x-1)(x-4)) = 1`

`4 - x+2x-8 = x^(2) - 5x + 4`

`x - 4 = x^(2) - 5x + 4`

`x^(2) -5x-x+4+4=0`

`x^(2) -6x+8=0`

`(x-4)(x-2)=0`

`x = 2, 4`