Answer:
The measure of the vertex angle is 100°
Explanation:
In Δ MNO
∵ Δ MNO is an isosceles triangle with base MO
∴ NM = NO
→ In an isosceles triangle, the base angles are equal in measures
∵ ∠M and ∠O are the base angles isosceles ΔMNO
∴ m∠M = m∠O
∵ m∠M = (3x + 10)°
∵ m∠O = (5x - 10)°
→ Equate their measures
∴ 5x - 10 = 3x + 10
→ Add 10 to both sides
∵ 5x - 10 + 10 = 3x + 10 + 10
∴ 5x = 3x + 20
→ Subtract 3x from both sides
∴ 5x - 3x = 3x - 3x + 20
∴ 2x = 20
→ Divide both sides by 2 to find x
∵
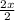 =
=
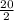
∴ x = 10
→ Substitute the value of x in the measures of ∠M and ∠O to find them
∵ m∠M = 3(10) + 10 = 30 + 10
∴ m∠M = 40°
∵ m∠O = 5(10) - 10 = 50 - 10
∴ m∠O = 40°
→ The sum of the measures of the interior angles of a Δ is 180°
∵ m∠M + m∠O + m∠N = 180°
∵ 40 + 40 + m∠N = 180
→ Add the like terms
∴ 80 + m∠N = 180
→ Subtract 80 from both sides
∴ 80 - 80 + m∠N = 180 - 80
∴ m∠N = 100°
∵ ∠N is the vertex angle of Δ MNO
∴ The measure of the vertex angle is 100°