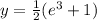Question

Solve for y.
ln(2y−1)=3

Answer y=(e^3+1/2)

for future reference

Answer 1

The correct answer is indeed y =
`(e^3+1)/(2)`

Explanation:

I also took the test!

Answer 2

The correct answer should be:

`y=(1)/(2)(e^3+1)\text{ or } y=(e^3)/(2)+(1)/(2)`

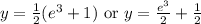
Explanation:

We have the equation:

`\ln(2y-1)=3`

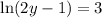
Let’s remove the natural logarithm by raising both sides to e. This yields:

`e^(\ln(2y-1))=e^3`

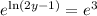
The left will simplify to:

`2y-1=e^3`

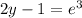
Add 1 to both sides:

`2y=e^3+1`

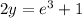
Divide both sides by 2. So, the value of y should be:

`y=(1)/(2)(e^3+1)`