Question

Miguel is designing shipping boxes that are rectangular prisms. One shape of the box with height h in feet, has a volume defined by the function V(h)=h(h-10(h-8). What is the height that would produce the maximum volume for the domain 0

Answer 1

`105ft^(3)`

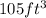
Explanation:

V(h) = h(–h + 10)(–h + 8)

Apply the distributive property to the right side and simplify.

V(h) = h(–h + 10)(–h + 8)

V(h) = {h(-h) + h(10)}(-h+8)

V(h) = (-h²+10h)(-h+8)

V(h) = (-h²)(-h) + (-h²)(8) + (10h)(-h) + (10h)(8)

V(h) = -8h² -10h² + 80h

V(h) = -18h² + 80h

Plug in the value of h from 1 to 9 (since 0<h<10) into the function V(h) = -18h² + 80h and create a table

h | V(h)

1 | 63

2 | 96

3 | 105 <------maximum volume is the highest y-value

4 | 96

5 | 75

6 | 48

7 | 21

8 | 0

9 | -9

The maximum volume for the domain 0<h<10 is 105 cubic feet.

Answer 2

Answer: 105ft^3

Explanation: