Given:
Polynomial is
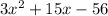 .
.
To find:
The sum of given polynomial and the square of the binomial (x-8) as a polynomial in standard form.
Solution:
The sum of given polynomial and the square of the binomial (x-8) is
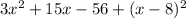
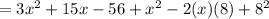
![[\because (a-b)^2=a^2-2ab+b^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ns8xcknd2la2h0fgcz5pt0lrf7e0cp5mva.png)
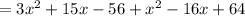
On combining like terms, we get
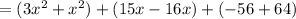

Therefore, the sum of given polynomial and the square of the binomial (x-8) as a polynomial in standard form is
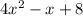 .
.