[1] 0.25, 0.25%, or
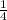
We will divide the number of wanted outcomes by possible outcomes.
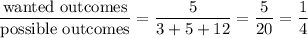
[2]
We will follow the same steps as problem 1.
MTHMTCS = 7 consonants
AEAI = 4 vowels
MTHEMTICS = 9 letters that are not A's
MATHEMATICS = total of 11 letters
(a)
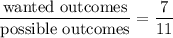
(b)
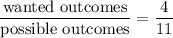
(c)
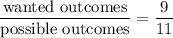
[3] 0.877
If the probability that a television is defective is 0.123, then the probability that a television is not defective is:
1 - 0.123 = 0.877