Question

Jennifer serves the volleyball to Marsha with an upward velocity of 10.5 ft/s. The ball is 5 feet above the ground when she strikes it. How long does Marsha have to

react, before the volleyball hits the ground? Round your answer to two decimal

Answer 1

0.98 seconds

Explanation:

We assume the height of the volleyball is described by the equation for ballistic motion. We want to find the time it takes for the height to become zero.

__

motion equation

The general form of the equation of height for ballistic motion is ...

`h(t)=-16t^2+v_0t+h_0\qquad\text{$v_0$ and $h_0$ are the initial velocity and height}`

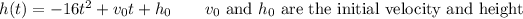
The coefficient 16 in the equation is an approximation of 1/2g, where g is the acceleration due to gravity in ft/s². This means the units of time and distance are expected to be seconds and feet.

For the problem at hand, the initial velocity and height are 10.5 ft/s and 5 ft. Then the height equation is ...

h(t) = -16t² +10.5t +5

__

reaction time

Marsha has until the ball hits the ground to react to the serve. To find out how long that is, we need to solve the height equation for t when h=0. This is most easily done using the quadratic formula with ...

• a = -16
• b = 10.5
• c = 5

The solution is ...

`t=(-b\pm√(b^2-4ac))/(2a)= (-10.5\pm√(10.5^2-4(-16)(5)))/(2(-16))\\\\=(10.5\pm√(430.25))/(32)=(21\pm√(1721))/(64)`

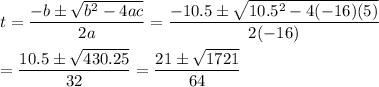
The positive solution is ...

t ≈ 0.976327 ≈ 0.98

Marsha has about 0.98 seconds to react before the volleyball hits the ground.

_____

Additional comment

After about 0.33 seconds, Marsha knows she doesn't need to react at all. The serve will not clear the net. Its maximum height is about 6' 8 5/8". A women's volleyball net is 7' 4 1/8" high. Jennifer's serve velocity must be at least 12.3 ft/s for the ball to go over the net. With that upward velocity, Marsha has about 1.06 seconds to react.