Question

A sample contains 20 kg of radioactive material. The decay constant of the material is 0.179 per second. If the amount of time that has passed

is 300 seconds, how much of the of the original material is still radioactive? Show all work

Answer 1

There are
`9.537* 10^(-23)` kilograms of radioactive material after 300 seconds.

Step-by-step explanation:

From Physics we know that radioactive materials decay at exponential rate, whose differential equation is:

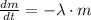`(dm)/(dt) = -\lambda\cdot m` (1)

Where:

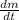`(dm)/(dt)` - Rate of change of the mass of the radioactive material, measured in kilograms per second.

`m` - Current mass of the radioactive material, measured in kilograms.

`\lambda` - Decay constant, measured in
`(1)/(s)`.

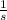The solution of the differential equation is:

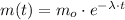`m(t) = m_(o)\cdot e^(-\lambda\cdot t)` (2)

Where:

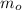`m_(o)` - Initial mass of the radioactive material, measured in kilograms.

`t` - Time, measured in seconds.

If we know that
`m_(o) = 20\,kg`,
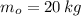`\lambda = 0.179\,(1)/(s)` and
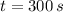`t = 300\,s`, then the initial mass of the radioactive material is:

`m(t) = (20\,kg)\cdot e^{-\left(0.179\,(1)/(s) \right)\cdot (300\,s)}`

`m(t) \approx 9.537* 10^(-23)\,kg`

There are
`9.537* 10^(-23)` kilograms of radioactive material after 300 seconds.