Answer:
Assumption: the angular acceleration of this flywheel is constant.
Angular acceleration:
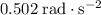 .
.
Net torque on this flywheel:
 (or, equivalently,
(or, equivalently,
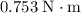 .)
.)
Step-by-step explanation:
Change in the angular velocity of this flywheel:
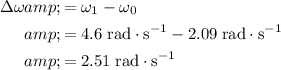 .
.
Divide this change in angular velocity
 with the duration
with the duration
 of the acceleration to find the average angular acceleration of this flywheel:
of the acceleration to find the average angular acceleration of this flywheel:
 .
.
By Newton's Second Law for Rotation, the net torque on this flywheel would be the product of the angular acceleration and the moment of inertia of this flywheel,
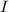 :
:
 .
.