Answer:
The wavelength of this sound wave would be longer in water than in the air.
Step-by-step explanation:
Let
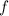 denote the frequency of this sound wave (standard unit:
denote the frequency of this sound wave (standard unit:
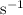 .)
.)
If the speed of sound in a particular medium is
 (standard unit:
(standard unit:
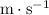 ,) the wavelength
,) the wavelength
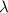 of this wave in that medium would be:
of this wave in that medium would be:
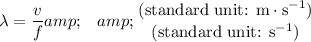 .
.
Let
 denote the speed of sound in water and let
denote the speed of sound in water and let
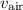 denote the speed of sound in the air at room temperature.
denote the speed of sound in the air at room temperature.
The wavelength of this sound wave in water would be:
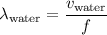 .
.
The wavelength of this sound wave in the air at room temperature would be:
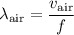 .
.
Fact: the speed of sound in water (a liquid) is greater than the speed of sound in air at room temperature. In other words:
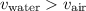 .
.
Given that
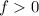 :
:
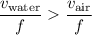 .
.
Therefore:
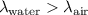 .
.