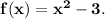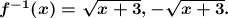Question

Cual es la función inversa de: f(x)=x2-3

Answer 1

f−1(x)=√x−3,−√x−3

Answer 2

Find the inverse function f(x)=x^2-3.

Replace f(x) with y.

y = x²-3

Swap the variables.

x = y²-3

Solve for y.

Rewrite the equation as y² - 3x = x.

Add 3 to both sides of the equation.

y² = x - 3

Take the square root on both sides of the equation to eliminate the exponent on the left side.

`\bf{y=\pm√(x+3) }`

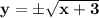
The complete solution is the result of the positive or negative portions of the solution.

First, use the positive value of ± to find the first solution.

`\bf{y=√(x+3) }`

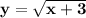
Then use the negative value of ± to find the second solution.

`\bf{y=-√(x+3) }`

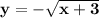
The complete solution is the result of the positive or negative portions of the solution.

`\bf{y=√(x+3) }`

`\bf{y=-√(x+3) }`

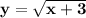
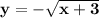
Solve for y and substitute with
`\bf{f^(-1)(x) }`.

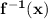substitute f⁻¹( x ) for y to show the final answer.

`\boldsymbol{f^(-1)(x)=√(x+3),-√(x+3) }`

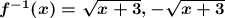
Set the composite results function.

`\boldsymbol{g(f(x)) }`

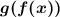
Evaluate g(f(x)) by substituting the value of f into g.

`\boldsymbol{\sqrt{(x^(2) -3)+3 } }`

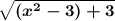
Add −3 and 3.

`\boldsymbol{g(x^(2) -3)=\sqrt{x^(2) +0} }`

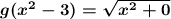
Add x² and 0.

`\boldsymbol{g(x^(2) -3)=\sqrt{x^(2)} }`

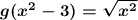
Extract terms from under the radical, assuming positive real numbers.

`\boldsymbol{g(x^(2) -3)=x }`

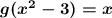
Given the
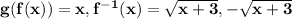`\bf{g(f(x))=x,f^(-1)(x)=√(x+3),-√(x+3) }` is the inverse of
`\bf{f(x)=x^(2) -3. }`

`\boldsymbol{f^(-1)(x)=√(x+3),-√(x+3). }`