The function f(x) = 2x2 + 3x + 5, when evaluated, gives a value of 19. What is the function’s input value?

Question

asked Sep 6, 2023 144k views

2 Answers

David Kristensen · Answer 1 · 2023-09-06T18:52:18+0000

Answer:

$x=2, \quad x=-(7)/(2)$

Explanation:

Set the function to 19:

$\implies 2x^2+3x+5=19$

Subtract 19 from both sides:

$\implies 2x^2+3x-14=0$

To factor a quadratic in the form
ax^2+bx+c

Find two numbers that multiply to
and sum to
: 7 and -4

Rewrite
as the sum of these two numbers:

$\implies 2x^2-4x+7x-14=0$

Factorize the first two terms and the last two terms separately:

$\implies 2x(x-2)+7(x-2)=0$

Factor out the common term (x - 2):

$\implies (2x+7)(x-2)=0$

Therefore the function's input values that when evaluated give a value of 19 are:

$(2x+7)=0 \implies x=-(7)/(2)$

$(x-2)=0 \implies x=2$

Dan Breen · Answer 2 · 2023-09-10T21:41:56+0000

Answer:

-7/2 or 2 are inputs that give 19 as output.

Explanation:

The problem gives us a quadratic function
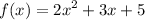$\displaystyle \large{f(x)=2x^2+3x+5}$ . When its output is 19, we want to know the input value(s).

Since an output which is f(x) = 19. Therefore:

$\displaystyle \large{19=2x^2+3x+5}$

Rearrange the expression in quadratic equation.

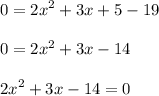
$\displaystyle \large{0=2x^2+3x+5-19}\\\\\displaystyle \large{0=2x^2+3x-14}\\\\\displaystyle \large{2x^2+3x-14=0}$

Factor the expression.

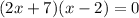
$\displaystyle \large{(2x+7)(x-2)=0}$

Solve like linear equation which we get:

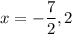
$\displaystyle \large{x=-(7)/(2), 2}$

If you input these x-values in the function, you will get 19 as the output which satisfies the condition.

Hence, inputs are -7/2, 2