Answer:
x = -2.5
x = 2
Explanation:
Hello!
We can remove the denominators by multiplying everything by it.
Solve:
Let's make one side equal to 0.
Solve by factoring, and then the zero product property.
Multiply 2 and -10. You get -20. Think of two number that multiply to -20, and add to 1. If we think about the standard form of a quadratic,
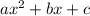 , think two numbers that equal "ac" and add up to "b".
, think two numbers that equal "ac" and add up to "b".
Using the zero product property, set each factor to 0 and solve for x.
- 2x + 5 = 0
2x = -5
x = -5/2 = -2.5 - x - 2 = 0
x = 2
The two answers are x = -2.5, and x = 2.