Answer:
Tabled Function
Explanation:
To determine which function is increasing the fastest over the interval [-5, 3], we need to calculate and compare each function's average rate of change over the given interval.
The average rate of change of function f(x) over the interval a ≤ x ≤ b is given by:
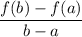
Given interval: -5 ≤ x ≤ 3
Therefore, a = -5 and b = 3
Tabled function
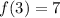
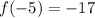

Equation: y = x² - 2


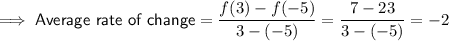
Graphed function
From inspection of the graph:

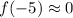
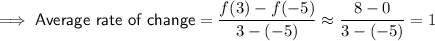
Therefore, the Tabled Function has the greatest average rate of change in the interval [-5, 3] and so it is increasing the fastest.