Answer:
m∠1 = 140°
m∠2 = 40°
m∠3 = 65°
m∠4 = 75°
m∠5 = 115°
Explanation:
We will use a few different methods to find the angles:
A triangle's angles will always add up to 180°. With this information, we can find the last angle of the triangle on the left:
∠1+∠2+∠3=180°
60+80+∠3=180°
Let x represent the value of ∠3. Simplify addition:
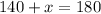
Subtract 140 from both sides:

The unknown angle is 40°. With this information, we can find the
m∠1:
m∠1 and the 40° we just found are supplementary angles, which means that their measures will add up to a total of 180°.
∠1+∠2=180°
Insert the value we know:
40°+∠2=180
Let x represent the value of ∠2. Subtract 40 from both sides:
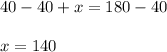
There fore:
m∠1=140°
We can use this same rule to find the m∠2:
∠1+∠2=180°
or, we can use the vertical angles rule. The first angle we found (Which is 40°) is a vertical angle to m∠2, so they have the same value. Therefore:
m∠2=40°
To find m∠3, we need to find the other missing angle in the middle triangle. Use the supplementary angle rule, since the missing angle is supplementary to the angle that is 105°:
∠1+∠2=180°
Insert the known values, substituting x for the unknown angle:
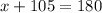
Subtract 105 from both sides:
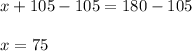
The unknown angle is 75°. Now find m∠3, knowing that triangles add up to 180°:
m∠2+m∠3+75=180
Insert the m∠2, make m∠3 be x:

Simplify addition:
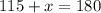
Subtract 115 from both sides:
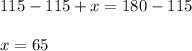
Therefore:
m∠3=65°
To find m∠4, use the vertical angle rule.
Therefore:
m∠4=75°
To find m∠5, we could find all triangle measures of the least triangle, or we can use the following:
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
The m∠5 is the exterior angle, and the opposite interior angles are 75° and 40°:
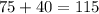
Therefore:
m∠5=115°
:Done