Answer:
Speed = 5.87m/s
Step-by-step explanation:
Given the following data;
Height of cliff = 45.1m
Horizontal distance = 17.8m
We know that acceleration due to gravity is 9.8m/²
Initial velocity = 0m/s
To find the time, we would use the second equation of motion;
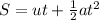
Substituting into the equation, we have;
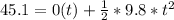
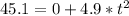
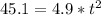


t = 3.034 secs
To find the speed;
Mathematically, speed is given by the equation;
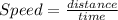
Substituting into the above equation;
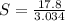
Speed = 5.87m/s
Therefore, the cliff diver must be running at 5.87 meters per seconds before jumping off the cliff.