Answer:
- 150π ft²
- 10π ft.
Explanation:
Area of the sector :
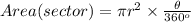
Finding the area given r = 30 ft. and θ = 60° :
⇒ Area = π × (30)² × 60/360
⇒ Area = π × 900/6
⇒ Area = 150π ft²
===========================================================
Length of the arc :
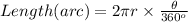
Finding the arc length given r = 30 ft. and θ = 60° :
⇒ Arc Length = 2 × π × 30 × 60/360
⇒ Arc Length = 60/6 × π
⇒ Arc Length = 10π ft.