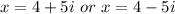Question

Use the quadratic formula to solve the
quadratic equation. SHOW ALL WORK.
2 −8+41 = 0

Answer 1

Solving the equation
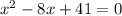`x^2-8x+41=0` using quadratic formula we get
`x=4+5i \ or \ x=4-5i`

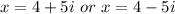
Explanation:

We need to solve the equation
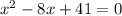`x^2-8x+41=0` using quadratic formula.

The quadratic formula is:

`$x=(-b\pm√(b^2-4ac))/(2a)$`

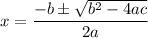
where a=1, b=-8 and c=41

Putting values in formula and finding x

`$x=(-b\pm√(b^2-4ac))/(2a)$\\$x=(-(-8)\pm√((-8)^2-4(1)(41)))/(2(1))$\\$x=(8\pm√(64-164))/(2)$\\$x=(8\pm√(-100))/(2)$\\We \ know \ √(-1)=i\\x=(8\pm10i)/(2)\\x=(8+10i)/(2) \ or \ x=(8-10i)/(2)\\x=4+5i \ or \ x=4-5i`

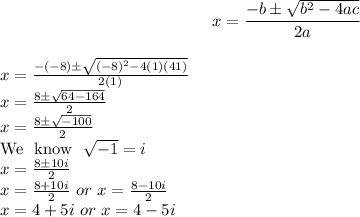
So, Solving the equation
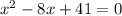`x^2-8x+41=0` using quadratic formula we get
`x=4+5i \ or \ x=4-5i`