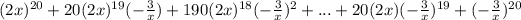Answer:
a)
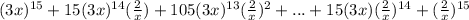
b)
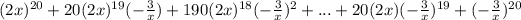
Explanation:
The binomial expansion formula is:
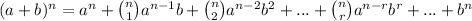
The (n r) in front of each term is the binomial coefficient. This can be calculated on a calculator using the nCr button (in this case, you'd put 15C1 for (n 1), 15C2 for (n 2), etc). This can be calculated without a calculator using this formula:
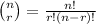
In a), a = 3x, b = 2/x and n = 15.
You can plug these into the formula above to get:
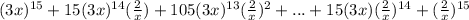
Here's how to do this without the formula:
- Start with the a^n
- In the second term, you subtract 1 from a's power (in this case, 15 to 14) and add 1 to b's power (0 to 1). Then you multiply it by nCr.
- This keeps going until you get to b^n. To check you've done it correctly, the powers of a and b in each term should add up to n. For example, in term 3 above, a's power is 13 and b's power is 2. These add to make 15.
- Remember, a's power goes down by 1 each time, and b's power goes up by 1 each time. There is no b in the first term because b^0 = 1.
You could 'simplify' this by expanding the brackets, but this gives you massive numbers so it's probably best to leave it like this.
Applying this to b):
a = 2x, b = -3/x, n = 20