Answer:
Part A)
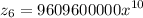
Part B)
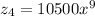
Explanation:
Recall the binomial expansion theorem:
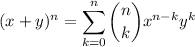
Part A)
Our expression is equivalent to:

To find the sixth term, let k = 5. Therefore, the sixth term is:
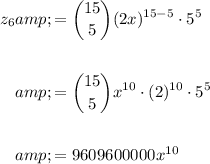
Part B)
Likewise:
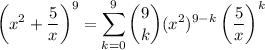
To find the fourth term, let k = 3. Therefore, the fourth term is:
