Given:
In triangle ABC, D is incenter m∠ACB = 3x + 54 and m∠ACD = x + 31.
To find:
m∠ACD.
Solution:
We know that,
Incenter of a triangle is the intersection point of all angle bisectors.
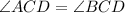 ...(i)
...(i)
Now,
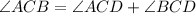
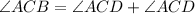 [Using (i)]
[Using (i)]
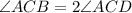
Substitute the values, we get
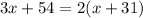

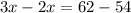
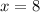
The value of x is 8.
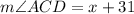
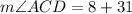

Therefore, the measure of angle ACD is 39 degrees.